Por su comportamiento eléctrico, pueden utilizarse en muchos circuitos que contengan señales de ciertas frecuencias los inductores y condensadores. Entre estos circuitos incluyen filtros, capaces de permitir el paso de las señales de ciertas frecuencias, bloquean ciertas señales de frecuencia, etcétera. Los filtros son aplicaciones generales que serán analizadas en este artículo.
Según sus características, los filtros pueden clasificarse en cuatro grupos:
a) Paso bajo
b) Paso alto
c) Pasa bandas o pasa faja
d) Rechazo de banda
El primero permite el paso de señales cuyas frecuencias están por debajo de cierto valor. El segundo permite el paso de las señales que están por encima de cierta frecuencia. El tercero permite el paso de señales que están dentro de un cierto rango de frecuencias y el cuarto rechaza las señales que están dentro de un cierto rango de frecuencias, dejando pasar lo demás.
Los filtros comunes están diseñados generalmente sobre con base en los componentes pasivos: inductores y capacitores.
En este artículo le dará una idea general de cómo filtros funcionan con estos componentes y analizar sus aplicaciones en filtros más adelante.
Capacitores
Los capacitores están formados por dos conjuntos de conductores de armadura separados por un material aislante, llamado dieléctrico.
Cuando se aplica un voltaje al capacitor, la armadura queda cargada con cargas de signos opuestos. La presencia de material aislante evita cualquier corriente pase a fluir entre la armadura y con ello quedarse sin cargas. La figura 1 muestra lo que ocurre.
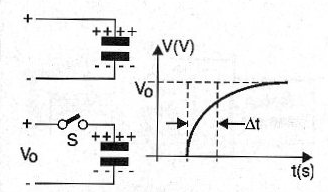
Esto significa que, una vez cargado, un circuito de CC (corriente continua), un capacitor representa una resistencia infinita. Ninguna corriente puede circular a través de él.
En circuitos de Corriente Alternada (CA), sin embargo, el comportamiento de un condensador es otro.
Al conectar un capacitor a una fuente de voltaje de corriente alternada (CA), como se muestra en la figura 2, el capacitor se carga y descarga tras las inversiones de polaridad de la tensión aplicada.
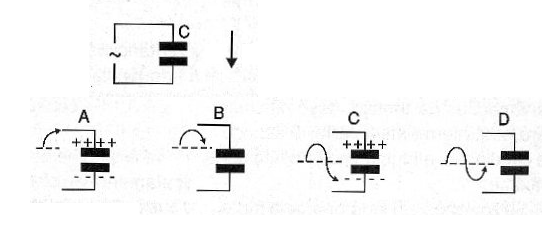
Esto significa que, diferentemente de la conexión en corriente continua donde la corriente no está circulando, siempre tendremos una circulación de corriente para carga y descarga del capacitor.
La intensidad de esta corriente depende de dos factores:
a) Valor del capacitor
b) Frecuencia da corriente del generador
Si el capacitor es pequeño, la cantidad de cargas eléctricas que debe moverse para cargar el capacitor es pequeña y la intensidad de corriente será menor. La intensidad de la corriente está en proporción directa al valor del capacitor.
Por otro lado, si la frecuencia del generador es mayor, tendremos una mayor velocidad de carga y descarga del capacitor y el movimiento de las cargas será mayor. La corriente estará en proporción directa al valor de la frecuencia.
Podemos imaginar un capacitor como un componente que presenta cierta "resistencia" al paso de una corriente alterna, pero no tienen en realidad ninguna carga pasando a través de ellos. Decimos, en términos más propios, que el capacitor presenta una "reactancia", y como este es el fenómeno decimos "reactancia capacitiva del capacitor”, como se muestra en la
Figura 3.
En la figura 3 mostramos un gráfico que relaciona la reactancia capacitiva con frecuencia.
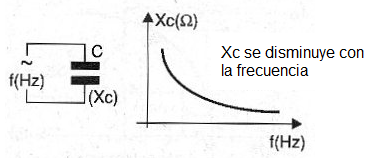
Una fórmula permite calcular la reactancia capacitiva de un capacitor, que se mide en ohms:
Xc = 1/(2 x π x f x C)
Donde:
Xc es la reactancia capacitiva en ohms
f é a frecuencia en hertz
C é a capacitancia en farads
π = 3,14 (constante)
Vea que, realmente, la resistencia que un capacitor presenta a circulación de una corriente es inversamente proporcional a la frecuencia y la capacitancia, como explicamos.
En la siguiente tabla, le damos algunos valores de reactancias y capacitancias asociadas para que el lector tienga alguna idea de su magnitud:
| f (kHz) | 1 uF | 1,5 uF | 2 uF | 2,5 uF |
| 10 | 159,236 | 106,157 | 79,618 | 63,694 |
| 20 | 76,618 | 53,079 | 39,809 | 31,848 |
| 30 | 53,079 | 35,836 | 26,539 | 21,232 |
| 40 | 39,809 | 26,540 | 19,905 | 14,924 |
| 50 | 31,847 | 21,230 | 15,924 | 12,740 |
| 60 | 26,539 | 17,693 | 13,270 | 10,616 |
| 70 | 22,748 | 15,165 | 11,374 | 9,098 |
| 80 | 19,905 | 13,270 | 9,953 | 7,962 |
| 90 | 17,693 | 11,795 | 8,847 | 7,078 |
| 100 | 15,924 | 10,615 | 7,962 | 5,370 |
Un capacitor de 1 uF, en la frecuencia de 50 kHz, por ejemplo, se comporta como una "resistencia" de 31,847 ohms.
Ejemplo de Aplicación de la Fórmula
¿Cuál es la reactancia capacitiva (Xc) presentada por un condensador (C)
de 1 uF a una señal de 2 kHz?
Tenemos:
Xc = ?
C = 1 x 10-6 F (convertiendo microfarads para farads)
f = 2 kHz = 2 000 Hz ou 2 x 103 Hz
Aplicando la fórmula:
Xc =1/(2 x 3,14 x f x C)
Xc = 1/(2 x 3,14 x 2 x 103 x 106 )
Xc = 1/(12,56 x 10-3 )
Xc = 0,0796 x 103
Xc = 79,6 ohms
INDUCTORES
Los inductores o bobinas muestran un comportamiento muy diferente de los capacitores, cuando se utiliza en un circuito de corriente alterna y corriente directa.
De hecho, si consideramos un inductor ideal, en el que el alambre de la resistencia utilizado en su devanado, como sugiere en la figura 4, vemos que una corriente puede circular a través de su devanado sin encontrar ninguna resistencia.
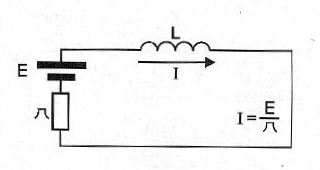
Sin embargo, en un circuito de corriente alterna, el comportamiento de un inductor es otro.
Para ilustrar lo que ocurre imaginamos un circuito en que un inductor se conecta a un generador de corriente directa a través de un interruptor, como se muestra en la figura 5.
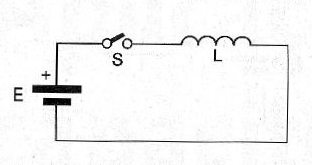
Cuando el interruptor es cerrado, se establece una corriente en el circuito. Sin embargo, esta corriente no alcanza su máxima intensidad inmediatamente.
La corriente, mientras circula la bobina del inductor crea un campo magnético cuyas líneas de fuerza, para expandir cortan las otras vueltas el mismo inductor.
El resultado es la inducción de una corriente que tiende a oponerse precisamente a esa que se está estableciendo. Con esto, la corriente no puede aumentar instantáneamente hasta el máximo permitido por el circuito. El inductor se opone a una rápida variación de la intensidad de corriente.
El gráfico que se muestra en la figura 6 muestra que la intensidad de la corriente crece según una curva exponencial lisa.
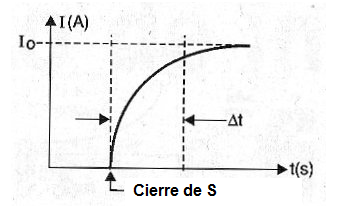
Podemos decir que "los inductores tienden a oponerse a las variaciones rápidas de corriente circulante".
En un circuito de corriente alterna, la tensión aplicada a un inductor varía constantemente y con eso la intensidad de corriente.
Por lo tanto, en este tipo de componente, la corriente debe aumentar hasta alcanzar un valor máximo, y, siguientes variaciones de tensión deberían disminuir para luego invertir la dirección del movimiento, llegando a un máximo.
Si conectamos un inductor a una fuente de tensión de CA (corriente alterna), como se muestra en la figura 7, la variación de tensión constante aplicada implica una oposición igualmente constante en la circulación de corriente a través del inductor.
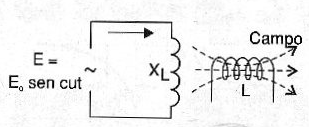
De la misma manera como en el caso de capacitores, esta oposición, llamada "reactancia inductiva" depende de dos factores:
a) Valor de inductancia del inductor l
b) Frecuencia de la tensión aplicada por el generador
Si el inductor es pequeño, es decir, tiene "pocas vueltas ", el campo magnético producido tendrá poca intensidad y sus líneas de fuerza no serán capaces de inducir una corriente mayor para oponerse a la circulación de corriente directa. La oposición será pequeña.
Si la frecuencia es alta, por otro lado, la variación de voltaje será rápido y la mayor oposición.
De todos modos, la oposición es mayor cuanto mayor sea la inductancia y la frecuencia de la señal aplicada.
También medir esa oposición a la corriente o inductiva reactancia en ohms.
Hay una fórmula para calcular la reactancia inductiva de un inductor o bobina dependiendo la inductancia y la frecuencia de la señal:
XL = 2 x π x f x L
Donde:
XL es la reactância indutiva em ohms
f es la frecuencia da corrente en hertz
L es la inductancia en henry
π es 3,14 – constante
Vea, en este caso, la reactancia es directamente proporcional a la frecuencia, lo que indica un comportamiento opuesto de capacitores.
Haciendo una comparación entre los dos componentes vemos que:
Mientras que los capacitores tienen menor oposición al paso de señales de alta frecuencia, los inductores ofrecen una mayor oposición a estas señales.
Los capacitores no dejen que las corrientes continuas pasen, que no ocurre con los inductores
Damos a continuación una tabla de reactancias inductivas para algunos valores comunes de inductancia y frecuencia, para que el lector tenga una idea de su magnitud:
| f (kHz) | 10 mH | 20 mH | 30 mH | 40 mH |
| 1 | 62,8 | 125,6 | 188,4 | 255,2 |
| 2 | 125,6 | 251,2 | 376,8 | 502,5 |
| 3 | 188,4 | 376,8 | 565,2 | 753,6 |
| 4 | 251,2 | 502,4 | 753,6 | 1004,8 |
| 5 | 314 | 628 | 942 | 1 256 |
| 6 | 376,8 | 753,6 | 1 130,4 | 1507 |
| 7 | 439,6 | 879,2 | 1 318,8 | 1 758,4 |
| 8 | 502,4 | 1 004,8 | 1 507,2 | 2 009,6 |
| 9 | 565,2 | 1 130,4 | 1 695,6 | 2 260,8 |
| 10 | 628 | 1 256 | 1 884 | 2 512 |
En la frecuencia de 2 kHz un inductor tiene una reactancia inductiva de
251,2 ohms.
Ejemplo de Aplicación de la Fórmula
¿Cuál es la reactancia inductiva (XL) por un inductor 100 mH en frecuencia de 5 kHz?
Tenemos:
XL = ?
L = 100 mH = 100 x 10-3 H
f = 5 kHz = 5 000 Hz = 5 x 103 Hz
Aplicando la formula:
XL = 2 x π x f x L
XL = 2 x 3,14 x 5 x 103 x 100 x 10-3
XL = 31,4 ohms




